Etude des fractales sur le bitcoin (BTC)

La question qui vient à l’esprit est de savoir si le bitcoin (BTC) est (ou non) un actif assez sensible aux phénomènes temporels. En ce sens, les fractales partent de l’hypothèse que ce qui se produit sur une période restreinte dans le passé peut se reproduire à plus grande ou moindre échelle dans l’avenir. Cette implication est extrêmement importante dans la mesure où les fractales démontrent aussi l’existence de cycles financiers. Aussi, cela remet en cause l’utilisation traditionnelle des probabilités. Ici, le cas du bitcoin (BTC) est intéressant pour observer le comportement d’un actif spéculatif. Pour cela, nous allons nous baser sur l’étude des fractales, et en particulier du coefficient de Hurst. Dans notre précédente publication, nous avions expliqué le principe du coefficient de Hurst. Lire : Exposant de Hurst et analyse financière – Cointribune. C’est un moyen de mesurer efficacement le comportement d’un actif à un moment donné. Assez naturellement, nous pouvons écrire que le bitcoin est un cas d’école…

Comment fonctionnent les fractales ?

On peut définir en deux lignes de calcul les fractales. Cependant, les explications sont souvent complexes et ambigües à ce sujet. On s’attachera ici à une compréhension la plus simple et la plus pédagogique à l’aide de cas d’exemple.

Fractales et probabilités…

Imaginons un actif fictif… Nous avons généré au hasard une liste de 245 données suivant une loi normale. Ces données représentent la variation d’un actif chaque mois. De manière arbitraire, on a défini la performance moyenne mensuelle de cet actif de +2,5 %, avec une volatilité de 5 %. C’est-à-dire que plus de deux tiers des variations prennent effet entre -2,5 % (2,5 – 5) et +7,5 % (5 + 2,5). En réalisant la distribution de ces variations, on obtient le graphique ci-dessous.

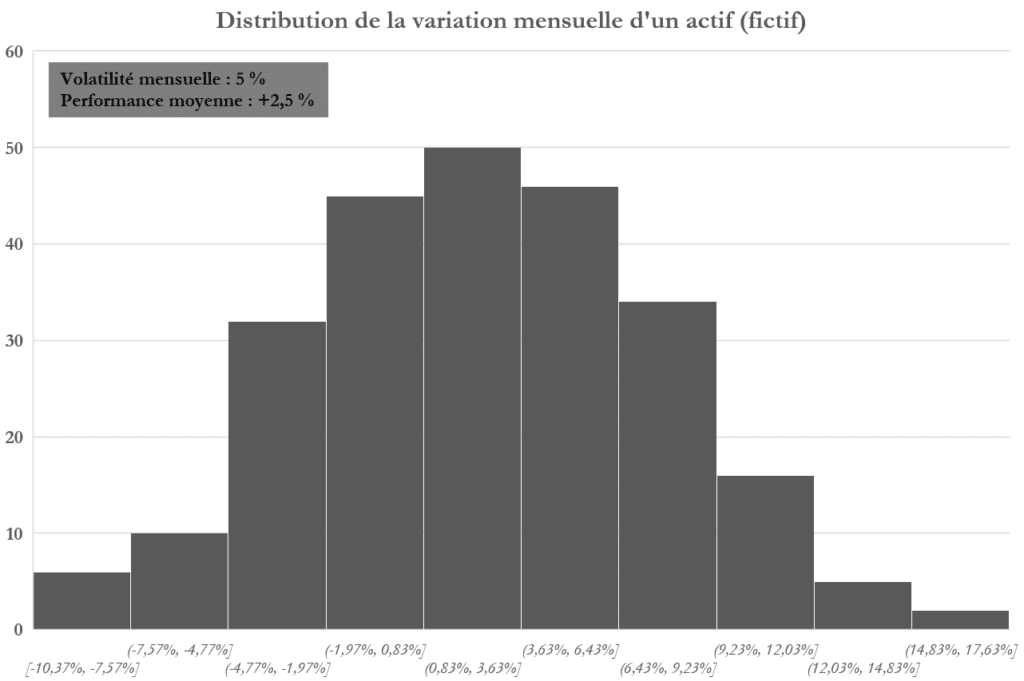
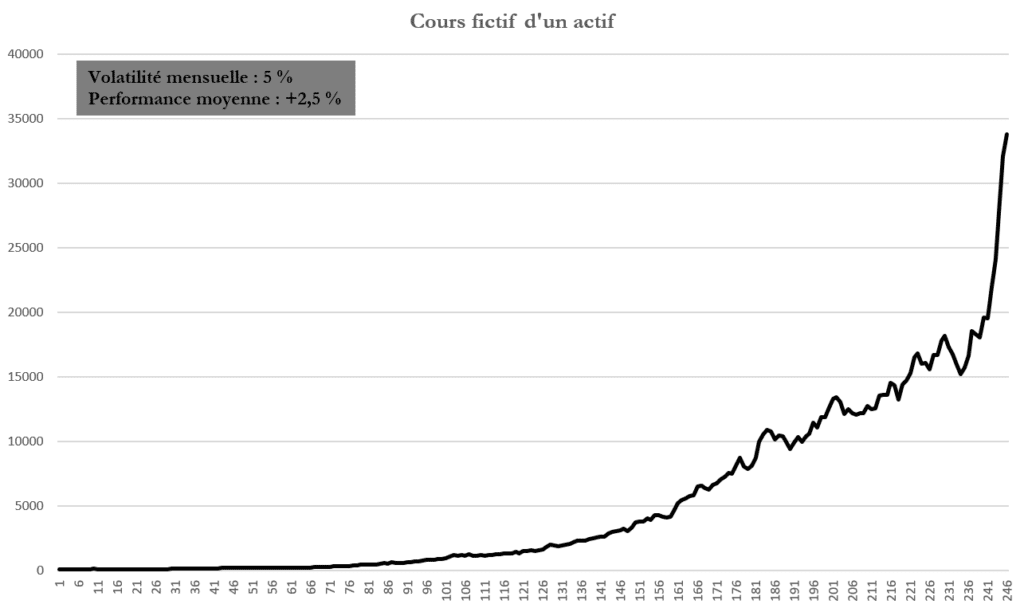
Pour plus de clarté, on a basé le cours initial de cet actif sur une base 100. On a ensuite appliqué les variations aléatoires générées pour représenter l’évolution « fictive » de cet actif. Le graphique ci-dessous montre ainsi des propriétés similaires au cours de nombreux actifs sur une échelle de plusieurs décennies. En l’espèce, les 245 mois de notre échantillon représentent l’équivalent de 20 ans et demi.

La mécanique du temps

En probabilités, on fait ce que l’on appelle une hypothèse de stationnarité. C’est-à-dire que les évolutions du passé sont non seulement indépendantes des évolutions du futur (discontinuité). Mais aussi que l’évolution de l’actif à long terme est reliée de manière tout à fait stationnaire (non cyclique) à l’évolution de court terme. Ainsi, notre actif fictif possède une volatilité mensuelle de 5 %. D’après cette hypothèse statistique, on cherche à calculer la volatilité annuelle. Voir plus sur le calcul de la volatilité : Calcul de la volatilité historique | Finance – Thomas Andrieu (andrieuthomas.com). Ainsi, on obtient que la volatilité annuelle (théorique) de cet actif est de 17 %.

Dans le détail (facultatif) du calcul, on fait la multiplication entre la volatilité mensuelle (5) et la racine carré du nombre de mois dans une année (période de référence). Ce calcul répond à l’hypothèse de « stationnarité » car on utilise ici la racine carré.

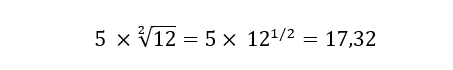
Mais voilà… Admettons que dans la réalité, la volatilité annuelle observée ne soit pas de 17 %, mais de 25 % ! Ce problème fut celui résolu par le mathématicien Benoît Mandelbrot. Et c’est ici que les fractales interviennent. Benoît Mandelbrot a d’abord fait l’hypothèse de non stationnarité de l’actif. En d’autres termes, il est parti de l’idée que le passé et le futur étaient influencés par des cycles qui modifiaient congénitalement la distribution de probabilité selon les époques. Et cette observation aura des conséquences révolutionnaires.

Résolution du problème de l’influence du temps

Revenons alors à notre exemple… La formule ne change pas, hormis à un détail près. D’un côté de l’équation, on sait que la volatilité annuelle est de 25 %. De l’autre, on sait que la volatilité mensuelle est de 5 %, et qu’il y aura toujours 12 mois dans l’année. Le paramètre à résoudre est donc de calculer ce fameux exposant (1/r ici). Il s’agit de l’exposant de Hurst !

Là encore, dans le détail (facultatif) du calcul, on résout l’équation suivante :

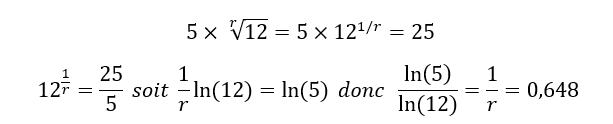
On obtient alors que l’exposant n’est pas de 1/2 comme dans l’hypothèse de stationnarité (racine carré), mais proche de 0,65. Dans l’analyse du coefficient de Hurst, cela signifie que l’actif est en tendance forte. En général, on observe sur la plupart des actifs que le coefficient de Hurst à long terme est proche de 0,6 et cela se traduit par l’existence de quelques cycles longs. Cela a pour conséquence que le long terme est toujours plus fiable que le moment présent.

Pour réaliser un calcul approximatif du coefficient de Hurst sur un actif, il suffit donc d’appliquer la formule de généralisation fournie par Benoît Mandelbrot. On calcule ainsi le ratio ln(P)/ln(t) ou P est la variation du prix (de la volatilité ici) d’une période sur l’autre et où t est le temps écoulé.

Le cas du bitcoin (BTC)

Comme dans notre exemple, nous allons utiliser le cas du bitcoin pour savoir si ce dernier est sensible au paramètre temporel à long terme. Notre étude se déroule en trois parties :

• On cherchera tout d’abord à estimer la probabilité mensuelle historique du bitcoin (BTC).
• Ensuite, on projettera la volatilité annuelle théorique du bitcoin.
• Enfin, on comparera cette volatilité avec la volatilité annuelle effectivement observée.
• On en déduira ainsi l’importance de la temporalité sur le bitcoin (BTC).

Etude des statistiques du bitcoin (BTC)

Dans le cas du bitcoin (BTC), on s’est basé de manière analogue sur les données mensuelles depuis septembre 2015 jusqu’à septembre 2022 (7 ans). Ainsi, la volatilité mensuelle mesurée sur le cours du bitcoin (BTC) est de 23,4 %. C’est-à-dire que plus de deux tiers des variations mensuelles prennent effet entre -15 % et +31 %.

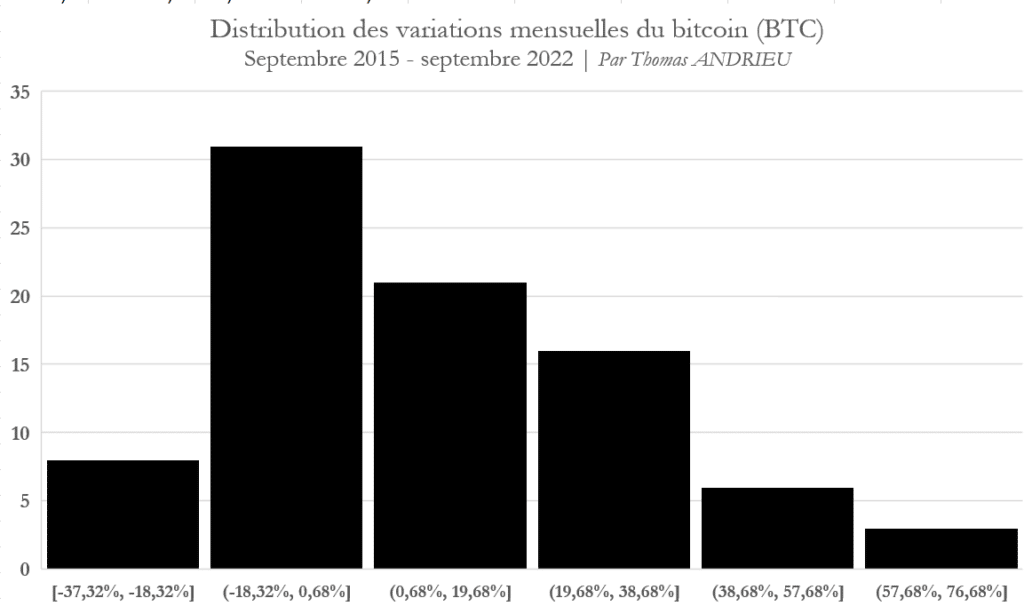
Cependant, il est assez intéressant de remarquer la distribution des variations du bitcoin. En effet, les variations mensuelles sont les plus fréquentes (36 % des variations) entre -18 % et 0 % par mois. Ensuite, plus la performance du bitcoin est élevée, moins cette observation est fréquente. De plus, la plupart des variations du bitcoin (BTC) sont biaisées dans la zone positive (> 0 %). En clair, le bitcoin (BTC) connaît de nombreux mois baissiers, mais la persistance de mois haussiers est plus ample et fréquente. De là naît le caractère extrême des mouvements du prix du bitcoin.

Annualisation de la volatilité (hypothèse de stationnarité)

Comme dans notre cas d’exemple, on réalise la multiplication entre 23,4 et la racine carré de 12. On obtient alors 81 % de volatilité annuelle… Mais ce résultat est bien loin de la réalité. Dans le graphique ci-dessous, nous avons représenté la variation sur un an du Bitcoin entre septembre 2016 et septembre 2022. En prenant une base annuelle, il apparaît que la volatilité n’est pas de 81 % mais de 232 % ! Sur une base continue, cette volatilité monte même à 300 %. Autant dire qu’il s’agit d’une volatilité absolument insignifiante dans l’étude des probabilités. Mais dans l’étude des fractales, cela nous permet de déduire l’importance du facteur temporel.

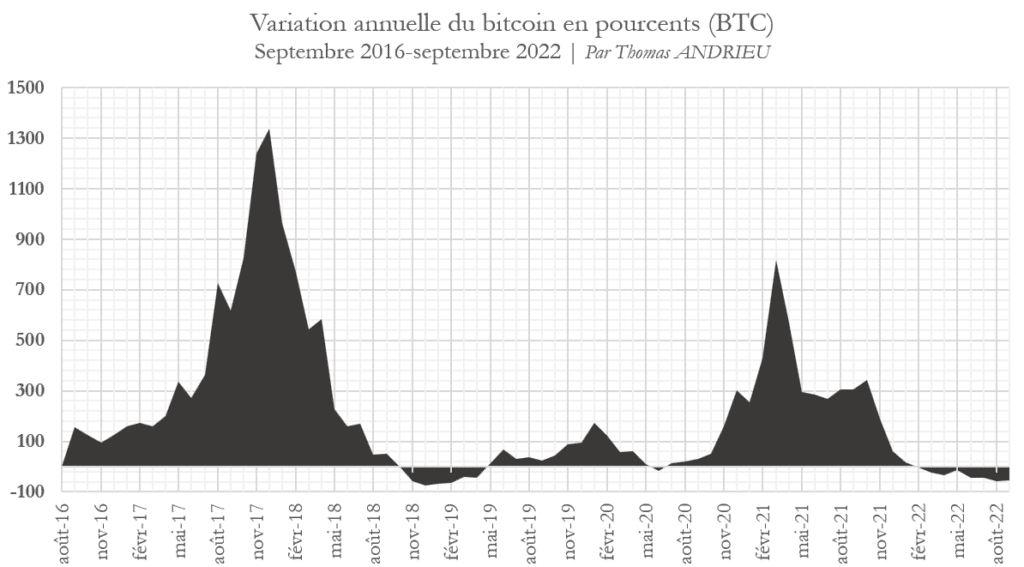
En outre, on remarquera le fait que la performance annuelle du bitcoin tend à diminuer depuis ses plus hauts historiques. A ce jour, le bitcoin (BTC) est proche de ses pires performances annuelles en comparaison à 2019.

Estimation du coefficient de Hurst

Une fois toutes ces données réunies, il nous est possible d’estimer la valeur du coefficient de Hurst sur le très long terme pour le bitcoin (BTC). En effet, on sait que la volatilité mensuelle est de 23,4 %, et que la volatilité annuelle observée est de plus de 230 %. On cherche alors à estimer la valeur du rapport 1/r comme dans le cas de notre exemple. Ainsi, dans le détail (facultatif), on a :

• Coefficient de Hurst (H) : H = ln(232/23,4) / ln(12) = ln(9,92) / ln(12) = 0,92

On en déduit donc que la valeur du coefficient de Hurst est de 0,92 et donc très proche de 1, et largement supérieure à 0,5. A long terme donc, le bitcoin (BTC) est dans une tendance extrême. Cela implique plusieurs conclusions sur lesquelles nous allons revenir.

En d’autres termes, cela revient à dire que le bitcoin n’est pas un actif qui suit des phénomènes aléatoires, mais bien des phénomènes cycliques. L’importance de la temporalité sur les cours est donc importante. De plus, la persistance d’une tendance extrême durable ne permet pas d’avoir de la visibilité statistique sur le très long terme.

Conséquences d’une forte influence du temps…

Nous avons vu qu’une très forte valeur de H signifie, à travers les fractales que le bitcoin (BTC) :

• C’est un actif où la temporalité est absolument déterminante. En effet, le comportement du prix du bitcoin est graduellement amplifié sur les échelles de temps plus longues. Il en résulte que la moindre période supplémentaire peut radicalement modifier le comportement du prix du bitcoin en rapport à la période précédente.
• C’est également un actif hautement cyclique. Ce cas de figure est caractéristique des actifs dont le prix est déterminé à long terme par de rares cycles très longs. Ces cycles ont une grande amplitude et une influence stratégique à mesure que leur nombre se réduit avec une plus grande échelle de temps.
• Dans une certaine mesure, on pourrait dire qu’en observant bien les mouvements à court terme du bitcoin (BTC), sur quelques semaines ou quelques mois, on peut remarquer les mêmes figures de prix que sur des échelles de plusieurs années ! Cela s’explique par les cycles, c’est aussi ce que l’on nomme comme les fractales. Benoît Mandelbrot parlait « d’auto force relative«  pour décrire ainsi les fractales.

Ainsi, le bitcoin (BTC) apparaît être un cas d’école extrêmement intéressant en ce qui concerne les fractales. On savait déjà que la plupart des actifs à long terme avaient un coefficient de Hurst autour de 0,6 ou parfois 0,7. Mais l’étude du bitcoin à long terme fait ressortir une extrême sensibilité au temps. Aussi, l’utilisation des modèles probabilistes pour décrire le comportement du bitcoin à long terme est absolument inutile. En conséquence, le recours aux fractales et aux cycles est indispensable.

En conclusion

Pour finir, nous avons rappelé que la mesure des fractales sur les marchés pouvait se faire de manière relativement simple. Parfois l’utilisation d’une simple calculatrice suffit… Dans notre cas, nous avons vu comment les fractales expliquaient bien mieux que les probabilités l’influence du facteur temps. L’idée selon laquelle la temporalité n’a pas d’influence sur les cours, c’est-à-dire que les cycles sont inexistants, est une idée absolument erronée. Les travaux de Benoît Mandelbrot à la fin du XXe siècle ont démontré en ce sens l’intérêt de l’étude des phénomènes « d’auto force relative ».

Dans le cas du bitcoin, il apparaît qu’il y a une claire incohérence mathématique si l’on considère que le temps n’a pas d’influence sur le comportement du bitcoin. En outre, la mesure de volatilité annuelle du bitcoin (BTC) nous donne des valeurs absolument excessives. L’étude des probabilités est donc impossible sur le bitcoin. Réciproquement, cela signifie que le bitcoin est un actif cyclique. La mesure du coefficient de Hurst pour le bitcoin démontre la présence d’une valeur supérieure à 0,9 !

En clair, le bitcoin est un actif cyclique. A ce jour, le bitcoin est dans une « tendance extrême » à long terme. La temporalité est un paramètre absolument déterminant pour la première cryptomonnaie mondiale. Le moment d’occurrence des tendances est aussi important que leur direction. En outre, on remarque que les schémas qui se produisent sur des échelles de temps très courtes sont aussi, dans une très large amplitude, les schémas qui se reproduisent dans le temps long. Le fait que le bitcoin soit dirigé par quelques cycles de long terme démontre avec brio le caractère hautement fractal de cet actif.