Bitcoin - Comment dérive-t-on les clés à partir des douze mots ?

Les wallets sont faits de telle façon qu’une simple douzaine de mots permet de reconstruire des milliers d’adresses. Comment ?

Wallet BIP-32

Après avoir vu dans cet article comment les wallets créent une seed, voyons à présent comment créer un wallet « HD ».

Les premiers wallets bitcoin comme Bitcoin-Qt étaient laborieux. Les clés étaient générées au hasard et stockées dans un fichier wallet.dat dont il fallait régulièrement faire la sauvegarde.

Depuis, les wallets sont devenus « HD » pour « Hierarchical » et « Deterministic ». Les adresses ne sont plus générées au hasard, mais de manière prédéfinie (deterministic) à partir d’une seule et même seed.

En sachant que derrière chaque adresse se trouve une clé publique. C’est important de le garder en tête. Une adresse n’est qu’un encodage de clé publique. C’est la même chose.

[Notre article sur le sujet : Comment les adresses Bitcoin sont-elles créées ?]

Ce concept de dérivation déterministe de clés fut introduit par Peter Wuille dans la BIP-32. En termes simples, une même seed produira toujours les mêmes paires de clés privées/publiques.

Si bien qu’une seule seed suffit pour restaurer des dizaines ou centaines de paires de clés auxquels vos BTC sont liés. Voire des millions dans le cas d’un exchange.

Notons avant d’aller plus loin qu’un wallet peut très bien fonctionner avec une seule paire de clés. Le problème étant la perte de confidentialité. Nous en avons parlé ICI. Il vaut donc mieux créer une nouvelle adresse (une nouvelle paire de clés) pour chaque transaction.

Dériver des clés à partir de la seed

Voici rapidement comment créer la seed originelle. Tout commence par la génération d’une « entropie » qui est un nombre aléatoire de 128, 256 ou 512 bits.

Reprenons l’entropie de 128 bits utilisée précédemment :

0 0 0 0 0 1 1 0 1 1 0 0 1 0 0 1 1 0 0 0 1 0 0 1 0 0 1 1 0 1 0 1 1 1 1 0 1 0 1 1 1 1 0 1 0 1 1 1 0 1 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 0 1 0 1 0 1 0 1 1 0 0 0 1 1 1 1 1 0 0 1 1 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 0 1 1 0 0 0 1 0 0 1 1 1 0 1 1 0 0 0 1 1 1 0 0 0 0 1

Ce nombre, exprimé ci-dessus en binaire (base 2), est généré de manière aléatoire. Ce qui, soit dit en passant, correspond au nombre 9 021 802 605 472 555 840 788 517 848 795 437 281 dans le système décimal (base 10).

Cette entropie sert à créer la phrase mnémonique (les 12 mots) qui sera dans notre cas :

Allow Equip essence Stuff Innocent Blue Fever Lamp Net Equip Invite Second

La phrase mnémonique est ensuite convertie en hash via la moulinette de la fonction de hachage HMAC-SHA-512. Ce hash est la fameuse seed de 512 bits :

b8485829b0151585b9c24ba336811b7274c08d0d44380028f01f7d7e5e5c2e26811cef5b44c9785ffae7341ed8ec6f079a77829136b148b72b73f70ea7d31c02

La seed est ici exprimée en hexadécimal (base 16) plutôt qu’en bits pour ne pas prendre trop de place.

Cette seed est ensuite scindée en deux pour créer la Master Private Key (m) ainsi que le Master Chain Code.

Les 256 bits de gauche font office de clé privée maîtresse :

b8485829b0151585b9c24ba336811b7274c08d0d44380028f01f7d7e5e5c2e26

Les 256 bits de droites font office du tout premier code de chaîne :

811cef5b44c9785ffae7341ed8ec6f079a77829136b148b72b73f70ea7d31c02

Simple non ? Illustration :

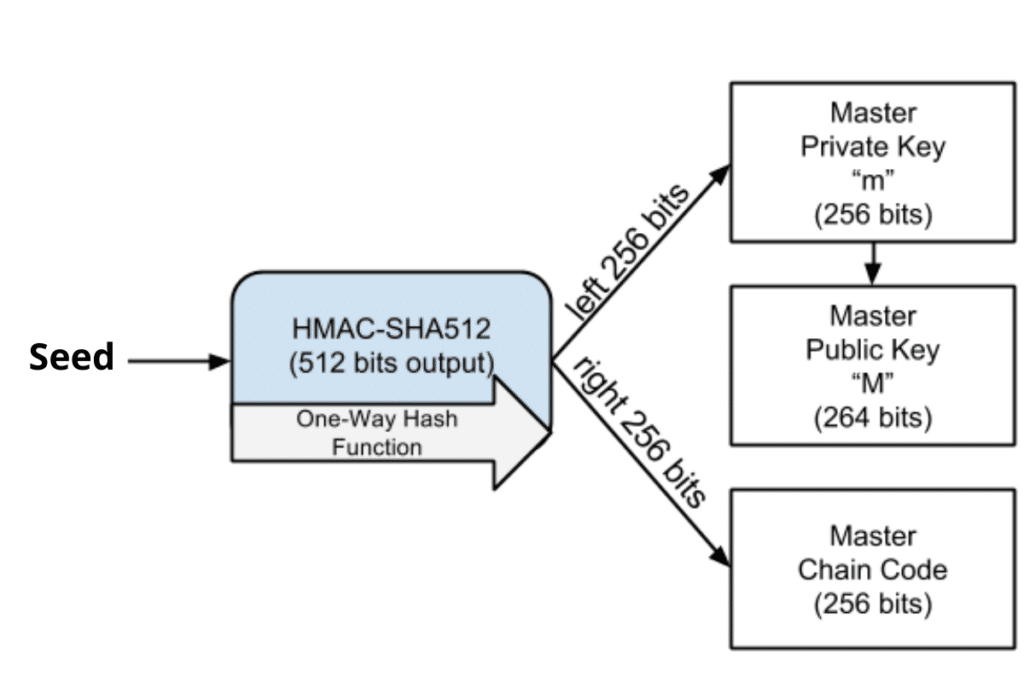
On génère ensuite à partir de la clé privée maîtresse (m) une clé publique maîtresse correspondante (M) à l’aide la cryptographie sur les courbes elliptiques. Cette partie est moins évidente, mais nous l’expliquerons prochainement.

Les autres paires de clés sont par suite créées de la même façon. Sauf qu’au lieu de partir de la seed, on part de la clé publique « étendue » (extended public key, ou « Xpub » dans le jargon).

Cette clé publique étendue combine :

-La clé publique maîtresse
-Un numéro d’index. La première clé dérivée aura l’index n° 0, la deuxième l’index n° 1, et ainsi de suite.
-Le code de chaîne.

Exemple de clé publique étendue :

xpub9v3zEm9W9QhLnMUEG9BkmpmGAf96uXh5NLMsdLWCVLur1fj26MY5ZjcXrb2aBF4U6uhzzs7Vw9jGopHxBYjsSmgozFBakbGiBgffGH

Ces trois informations mises bout à bout forment une clé publique « étendue » qui sera de nouveau hachée par HMAC-SHA-512 dont le hash résultant sera encore séparé en deux moitiés de 256 bits. L’une forme la clé privée fille (en lui accolant la clé privée maîtresse) et l’autre un nouveau code de chaîne.

Les 256 bits de droite de la sortie du hachage deviennent le code de chaîne de l’enfant. Les 256 bits de gauche du hachage sont ajoutés à la clé du parent pour produire la clé privée de l’enfant.

La modification de l’index permet d’étendre le nombre de clés filles 1,2,3, etc. Chaque clé étendue peut générer plus de deux milliards de clés filles. Et donc autant d’adresses bitcoin.

Et chaque clé fille peut servir à créer une clé étendue à partir de laquelle une nouvelle série de clés filles (une nouvelle branche) pourra être dérivée :

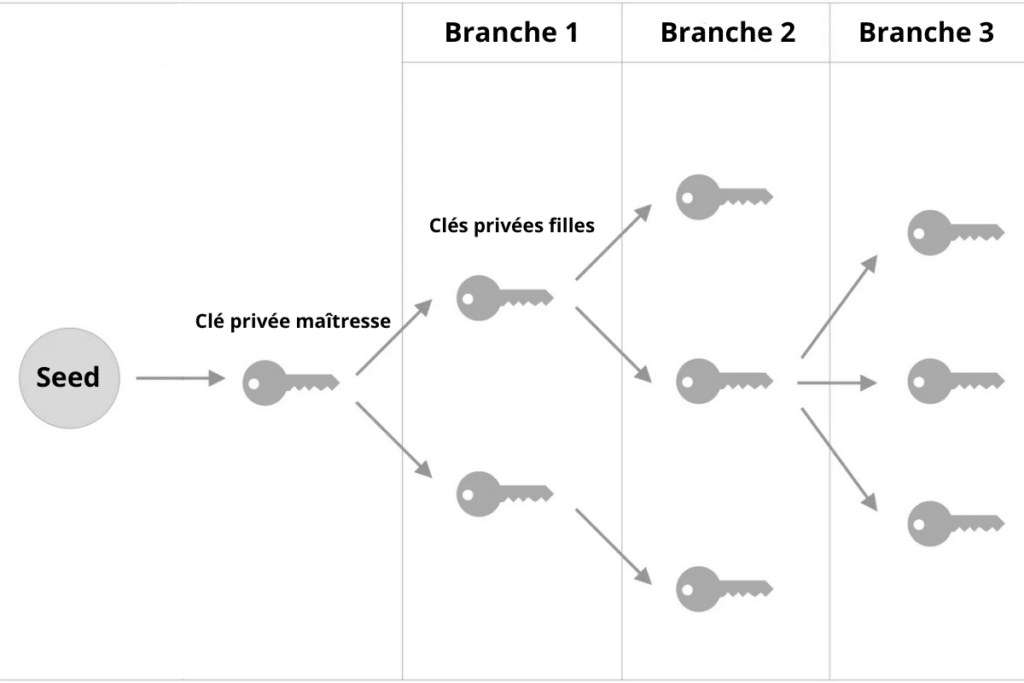
Voilà pourquoi BIP-32 permet de récupérer tous ses bitcoins à partir d’une simple douzaine de mots.

Et vu que tous les wallets ont adopté ce protocole, vous pouvez également changer de wallet comme de chemise avec la même seed.